- What is
a "normal" distribution?
- The
distribution of equally-likely events in the long run
through accidents of nature.
- In an
infinite amount of time, a random process could
ultimately generate structured results: e.g., a group
of monkeys seated at typewriters could peck out all
the great works of literature.
- This
would be an extremely rare event, but it is
conceivable.
- The
normal curve is a mathematical formula that assigns
probabilities to the occurrence of rare events.
- Statistically
speaking, it is a probability distribution for a
continuous random variable:
- The
ordinate represents the probability density for the
occurrence of a value.
- The
baseline represents the values.
- The
exact shape of the curve is given by a complicated
formula that you do NOT need to know.
- The
area under the curve is interpreted as representing
all occurrences of the variable, X.
- We
can consider the area as representing 100 PERCENT
of the occurrences; in PROPORTIONS this is
expressed as 1.0.
- We
can then interpret AREAS under the curve as
representing certain PROPORTIONS of occurrences or
"probabilities".
- We
cannot assign a probability to any point, but we
can attach probabilities to INTERVALS on the
baseline associated with AREAS under the curve:
e.g., the mean has 50% of the cases standing to
each side.
-
-
Special
properties of the normal distribution:
- Their
shape is such that it
- Embraces
68.26% of the cases within 1 s.d.
around the mean.
- Embraces
95.46% of the cases within 2 s.d.
around the mean.
- Embraces
99.74% of the cases within 3 s.d.
around the mean.
- More
roughly speaking, 68%, 95%, and 99% of
the cases are embraced within 1, 2, and
3 standard deviations from the mean in a normal
distribution.
- Determining
whether a distribution is "normal"
- The
"Eyeball" test
- Is
the distribution unimodal?
- Is
the distribution symmetrical?
- More
exacting mathematical tests: measured according to
"moments" or "deviations" from the mean
- FIRST
MOMENT:
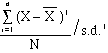= 0 <----you know this
already
- SECOND
MOMENT:
= variance <--- you had this
- THIRD
MOMENT:
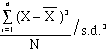= skewness
- Formula
calculated within SPSS
- Positive
values greater than 0 mean
right-skew
- FOURTH
MOMENT:
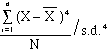- 3 = kurtosis
- Positive
values means more peaked (LEPTOKURDIC)
than the normal curve
- Negative
values means flatter (PLATYKURDIC)
- If
skewness and kurtosis values tend toward 0, then the
distribution approximates a normal
distribution.
- Suppose
the distribution is not normal?
- No
matter how the original observations are
distributed, the mean plus or minus two standard
deviations will include at least 75% of the
observations.
- No
matter how the original observations are
distributed, the mean plus or minus three standard
deviations witll include 89% or more. (Freeman, p.
62)
-
-
Using the Table of Areas under the Normal Curve: The
z-score
- One
determines the probability of occurrence of a random
event in a normal distribution by consulting a
tables
of areas under a normal curve (e.g., Table
D.2, pp.702-705 in Kirk).
- Tables
of the normal curve have a mean of 0 and a standard
deviation of 1.
- To use
the table., you must convert your data to have a mean
of 0 and standard deviation of 1.
- This is
done by transforming your raw values into z-scores,
according to this formula:
- z-score =
|
Example:
percent black in Washington, D.C. in 1980
(Note: not 1990)
|
|
D.C's
Raw score = 70.3
|
|
|
|
Mean
for all states = 10.3
|
|
|
|
|
(70.3
- 10.3) = 60
|
60 / 12.5 = 4.8
|
|
|
standard
deviation = 12.5
|
|
|
|
z-score
for D.C. = 4.8
|
|
Example:
D.C.'s percent vote for Reagan in
1984
|
|
D.C's
Raw score = 13
|
|
|
|
Mean
for all states = 60
|
|
|
|
|
(13
- 60) = 47
|
47 / 8.8 = -5.3
|
|
|
standard
deviation = 8.8
|
|
|
|
z-score
for D.C. = -5.3
|
|
Comparison
with Florida: percent vote for Reagan in
1984
|
|
Florida's
percent black is 13.8
|
|
|
|
z-score
= (13.8 - 10.3) / 12.5 = .28
|
|
Florida's
percent for Reagan was 65
|
|
|
|
z-score
= (65 - 60) / 8.8 = .57
|
|
-
- Computing
z-scores for raw data Transforming raw
standardizes the data, which makes it easier to
compare values in different distributions.
-
- Limitations
of raw data values
- Raw
scores of individual cases do not disclose how they
vary from the central tendency of the
distribution
- One
needs to know also the mean of the distribution and
its variability to determine if any given score is
"far" from the mean
- Properties
of the z-score transformation
- It is a
LINEAR transformation: does not alter relative
positions of observations in the distribution nor
change the shape of the original
distribution.
-
- The
transformed observations have positive AND negative
DECIMAL values expressed in STANDARD DEVIATION
UNITS.
- The
SIGN of the z-score tells whether the observation
is above or below the mean.
- The
VALUE of the z-score tells how far above or below
it is.
- When transformed into z-scores, all distributions are
standardized
- The
mean of the transformed distribution is equal to
0.
- The
standard deviation of the distribution is equal to
1.
- The
variance of the distribution is equal to 1. (Old
Chinese proverb.)
- When
subjected to a z-score transformation, any set of raw
scores that conform to a normal distribution, will
conform exactly to the table of areas under the normal
curve.
- That
is, the likelihood of observing z-scores of certain
magnitudes can be read directly from Table D.2.
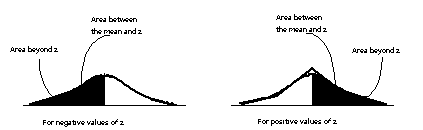
- Using
z-scores to
read a
table of areas under the normal
curve
|